Dentro de una máquina eléctrica, se observa la compleja geometría interna de estatores ranurados, rotores con imanes o polos bobinados y una intrincada distribución de conductores. En muy raras ocasiones, el rotor es un cilindro circular isótropo homogéneo. Tanto el rotor como el estator podrían describirse como conjuntos de componentes discretos con diferentes formas y tamaños. Si se busca regularidad, se podría contar la cantidad de ranuras y pares de polos, solo para descubrir que no son iguales; lo que es peor, es posible que ni siquiera tengan un factor común. Por ejemplo, una máquina de doce ranuras y diez polos tiene doce ranuras y cinco pares de polos, sin factor común. ¿Cómo puede esta configuración producir un par constante?
La pregunta se vuelve aún más compleja tras examinar el controlador electrónico de potencia de campo orientado (driver) que se utiliza en máquinas modernas. En él, encontramos componentes discretos que operan en modo conmutado (lo que significa que los transistores de potencia están activados o desactivados, nunca funcionando en un modo lineal controlado). ¿Cómo se puede, entonces, obtener un par uniforme con un sistema así?
La respuesta corta es que, en casi todas las máquinas eléctricas, un par absolutamente constante es prácticamente inalcanzable, y cierto grado de rizado de par es inherente. El arte del diseñador consiste en reducirlo a un nivel aceptable. A menudo, este nivel es muy bajo, y en algunos casos puede ser tan bajo que resulta difícil de medir.

Es útil dividir el tema en una cuestión de armónicos. La ondulación de par es un armónico no deseado del par del eje (que, si fuera perfectamente uniforme, tendría un valor promedio de orden armónico cero). Tiende a causar ondulación de velocidad, que es un armónico no deseado en la velocidad. En muchos casos, la inercia rotatoria actúa como un filtro mecánico de paso bajo simple, adecuado para atenuar la ondulación de velocidad. Sin embargo, en sistemas más complejos, la ondulación de velocidad puede verse peligrosamente amplificada por resonancias torsionales con órdenes armónicos específicos.
La resonancia puede amplificar los armónicos de par, lo que resulta en un patrón de tensión torsional cíclica en el eje y los acoplamientos, lo que a su vez puede causar fallos por fatiga o el aflojamiento de tuercas y tornillos. La ondulación de par suele estar asociada con la vibración (y el ruido), que puede ser difícil de resolver únicamente mediante el diseño mecánico. Si no se puede confiar en la inercia para mitigar los efectos de la ondulación del par, se debe reducir en la fuente.
Uno de esos sagrados conjuros de ingeniería que todos los estudiantes murmuran fuera del aula de exámenes es que «El par es igual al flujo por la corriente». Por lo tanto, se debe suprimir los armónicos tanto en el flujo como en la corriente. Pero ¿dónde se encuentran y cómo interactúan?
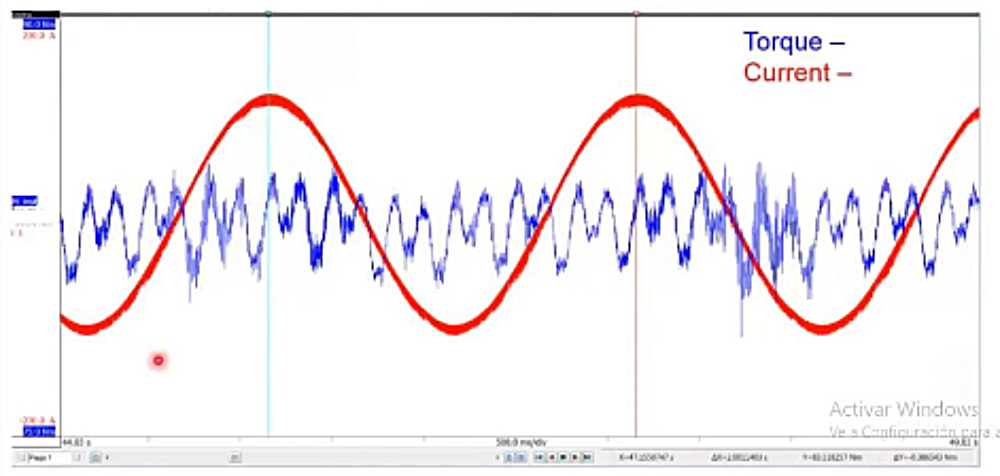
Se puede empezar diciendo simplemente que, para las máquinas de corriente alterna, la forma de onda temporal de la corriente debe ser lo más cercana posible a una onda sinusoidal pura. En las máquinas alimentadas por inversor, esta es la función del regulador de corriente y su algoritmo de control. La inductancia actúa como un filtro paso bajo simple que ayuda a reducir los armónicos no deseados (especialmente en la frecuencia portadora) en la forma de onda de la corriente, de forma análoga al filtrado mecánico de la inercia rotacional en relación con la velocidad.

Pero el concepto de "armónicos de flujo" no es tan simple. Se tiene que estudiar el producto "flujo por corriente" en términos de la interacción de las distribuciones de flujo y corriente dentro de la máquina.
En la teoría clásica, estas distribuciones se resuelven en la distribución de densidad de flujo y la distribución de amperes-conductor del estator alrededor del entrehierro. Usaré estos conceptos fácilmente visualizables a lo largo de este escrito. Pero debo hacer la observación de que la composición armónica de estas distribuciones no es el resultado inmediato de un análisis de elementos finitos.
Esto lleva a la pregunta de si el par debe analizarse en términos de estas distribuciones armónicas, o si debe calcularse por la tensión de Maxwell (que es el resultado inmediato de un análisis de elementos finitos). Las distribuciones armónicas conducen directamente al par promedio temporal (a menudo, mediante un análisis de elementos finitos en una sola posición del rotor), mientras que la tensión de Maxwell proporciona el par instantáneo en una sola posición del rotor y, por lo tanto, debe repetirse durante un ciclo completo para obtener el par promedio o de funcionamiento. Sin embargo, a pesar de sus obvias diferencias, ambos enfoques son más compatibles de lo que podría parecer a primera vista, como se verá. (Véase también [3] y [4]).
Para las máquinas de corriente alterna, se utilizan series de Fourier para analizar los armónicos espaciales de la distribución del devanado, la distribución del flujo y, en ocasiones, la distribución de la permeancia dentro de la máquina, a lo largo de la dirección circunferencial alrededor del entrehierro. (También se utilizan series de Fourier para analizar los armónicos temporales en la forma de onda de la corriente, a veces en base a la teoría de componentes simétricos en casos de funcionamiento desequilibrado; pero en este caso procederé con el supuesto de corrientes polifásicas sinusoidales equilibradas).
El par se obtiene de la integral (con respecto al ángulo alrededor del entrehierro) del producto de dos series armónicas: una que representa la distribución ampere-conductor del estator y otra que representa algún atributo productor de par del rotor, que se puede llamar "el flujo del rotor". (Esto podría ser el resultado de imanes o devanados de campo o saliencia, o alguna combinación, y el término "flujo del rotor" será familiar especialmente para los ingenieros de control orientados al campo, que lo usan incluso con motores de inducción).
El producto de estas ondas es una onda de esfuerzo cortante en la superficie del rotor, cuya integral sobre 360° es esencialmente el par instantáneo. El principio central en la producción de par es notable, siendo que un resultado distinto de cero para esta integral (y por lo tanto el par) se produce solamente por la interacción de los armónicos del espacio de trabajo de la distribución ampere-conductor del estator y el flujo del rotor (a veces llamados “armónicos fundamentales").
Ninguna de las demás interacciones armónicas espaciales produce par neto (siempre que las formas de onda de la corriente sean ondas sinusoidales equilibradas). Este notable hecho se deriva directamente del principio de ortogonalidad en relación con el producto de dos series de Fourier, y representa el extraordinario efecto de filtrado que se produce de forma natural en la configuración de las máquinas de corriente alterna.
Esto significa que, para calcular el par medio, es posible centrarse en los armónicos de trabajo de la distribución de amperes-conductor del estator y el flujo del rotor, e ignorar todos los demás armónicos espaciales. Esta es la base de la transformación del eje dq (transformada de Park). El desarrollo teórico de la transformada de Park parte del supuesto de distribuciones espaciales sinusoidales de flujo y amperes-conductores alrededor del entrehierro. Y aunque no trabaja con armónicos espaciales de ninguno de los dos, reconoce su existencia al agrupar sus efectos inductivos en la inductancia de fuga armónica o inductancia diferencial, mientras que no contribuyen en nada al par.
Las distribuciones espaciales armónicas de trabajo de los conductores de amperes del estator y el flujo del rotor giran en sincronismo a la velocidad síncrona, y Park las proyecta sobre un sistema de referencia que gira a velocidad síncrona. En este sistema de referencia (los llamados “ejes dq”) todo parece constante en funcionamiento estacionario. Por ello, Park representa los efectos distribuidos de los conductores de amperes del estator y el flujo del rotor mediante las magnitudes terminales, la corriente y el enlace de flujo. Para proporcionar un medio de orientación (modificando el ángulo de fase espacial relativo entre el flujo y las distribuciones de amperes-conductores del estator), Park necesita dos bobinas o devanados: uno alineado con el eje d o eje de campo del rotor y el otro alineado con el eje q o eje de cuadratura, perpendicularmente al eje d. De esta manera, obtiene una relación de flujo ψ y una corriente i, ambos con subíndice d1 para el devanado del eje d, y con subíndice q1 para el devanado del eje q. El subíndice adicional refleja que las distribuciones respectivas son los armónicos del espacio de trabajo del flujo y los amperios-conductores.
El par electromagnético promedio se obtiene ahora a partir de la ecuación:

T = 3/2 p (ψ_d1i_q1 - ψ_q1i_d1)

donde “p” es la cantidad de pares de polos. En el lenguaje coloquial moderno, se puede describir esto como "increíblemente simple" en vista de la complejidad del sistema físico y su análisis matemático. Este es el E = mc² del diseño de máquinas eléctricas. Su derivación a menudo se pierde en matices analíticos, pero el mantra del estudiante es claro: par = flujo × corriente.

Hay que embellecerlo ligeramente. Primero, se necesita el flujo por la corriente para ambos ejes del modelo dq, no solo para uno de ellos. En segundo lugar, hay que distinguir el flujo ligado (una magnitud terminal o de circuito) del flujo (una magnitud distribuida o de campo). En tercer lugar, sumar los coeficientes 3/2 y p. No entraré en la interpretación de estos coeficientes, ni siquiera discutiré las unidades de la ecuación, sino simplemente reflexionaré sobre su increíble simplicidad.
¿Se puede usar esta elegante ecuación de par con análisis de elementos finitos en una sola posición del rotor, en lugar de una simulación total completa de escalonamiento de la posición del rotor con tensión de Maxwell? La respuesta es sí; se pueden encontrar ejemplos en [3] y [4], entre otros. Pero, por supuesto, solamente proporciona el par promedio o de funcionamiento, sin rizado, sin dentado ni efectos parásitos (como pérdidas parásitas y contribuciones de fuga armónica a la inductancia terminal).
Las bobinas de los ejes d y q, que representan el devanado del estator polifásico real, tienen una distribución sinusoidal, en el sentido de que sus distribuciones espaciales (circunferenciales) de amperes-conductor son sinusoidales, con solo el número armónico de trabajo o fundamental de pares de polos p. Pero sus inductancias se complementan con la inductancia de fuga mencionada anteriormente, que incluye la fuga armónica asociada a los demás armónicos espaciales de los devanados. Esto es necesario para que el modelo del eje dq pueda producir las tensiones terminales correctas (mediante las denominadas “ecuaciones de Park”). La inductancia asociada al armónico espacial de trabajo de las distribuciones ampere-conductor del eje dq se denomina «inductancia magnetizante», mientras que la inductancia total del devanado del eje d es la inductancia síncrona Ld, y también Lq para el devanado del eje q.
Todas estas ideas son muy antiguas y se han utilizado como base del diseño de máquinas eléctricas durante más de un siglo. Han pasado cien años desde que se publicó la transformada del eje dq de Park y más de ciento treinta desde que Blondel publicó su teoría de dos reacciones, que también se basa en la noción de distribuciones sinusoidales de ampere-conductores y flujo.
La expresión moderna de estos principios a menudo se da en términos de vectores espaciales, el lenguaje del control orientado al campo; mientras que los elementos reales (en particular, el enlace de flujo, la inductancia y el torque) se calculan mediante análisis numérico con una precisión y un conocimiento muy superiores a los que estaban disponibles en los primeros tiempos.
Es fácil olvidar que la transformada del eje dq de Park se basa en el análisis de series de Fourier de las distribuciones de flujo y ampere-conductor, aunque es claramente obvio cuando se aplica a la matriz de inductancia en la derivación de Ld y Lq, [2,3]. Pero en términos matemáticos, el análisis armónico por series de Fourier es una operación lineal. Al "agregar” armónicos, encarna el principio de superposición y, por lo tanto, su validez (o al menos su precisión) puede cuestionarse cuando se aplica a un sistema no lineal como una máquina eléctrica. Se podría imaginar que el enfoque de simulación total no se ve afectado por esta preocupación, y eso ciertamente sería cierto para el cálculo del torque por la tensión de Maxwell.
También sería perfectamente válido descomponer una forma de onda de torque en sus componentes armónicos usando series de Fourier, después de haber sido calculada por la tensión de Maxwell en una simulación total que no usó la transformada de Park.
Pero es común, incluso en el enfoque de simulación total, usar Ld y Lq y las ecuaciones del circuito de Park sin detenerse a considerar si la descomposición armónica subyacente a la transformada de Park es completamente válida. Incluso si el principio de superposición es aceptable en relación con la composición armónica del flujo y las distribuciones de amperes-conductor, sigue siendo el caso de que los armónicos en estas distribuciones introducen variaciones armónicas en Ld y Lq.
En otras palabras, pueden variar con la posición del rotor. Parece que rara vez reconocemos esta posibilidad. En cambio, navegamos a través de nuestro diseño de máquina y nuestro análisis con la suposición tácita de que Ld y Lq son independientes de la posición del rotor, aunque aceptamos fácilmente su variación con la corriente.
Parece funcionar. ¡Tal vez sea debido al conocimiento acerca de los diseños de bobinados y la adherencia a las mejores prácticas! Sin embargo, hay ingenieros que no confían del todo en las suposiciones subyacentes, por lo que recurren al enfoque de simulación total para todo, incluso para el análisis de circuitos. Los ingenieros de esta escuela de pensamiento bien podrían ser los primeros en describir la simplicidad de la ecuación de par como “increíble”, y tendrían razón, aunque el término “increíble” sea un poco extremo. Quizás tengan razón. La alternativa de la simulación total solo es posible, por supuesto, con el software de simulación más potente; ciertamente no era posible hace una generación. Un análisis completo de estos temas interrelacionados sería una tarea difícil y compleja para un estudiante de doctorado; y, francamente, no sé si se ha abordado ni en qué medida. El abanico completo de preguntas e implicaciones teóricas parecería estar fuera del alcance habitual de nuestro ajetreado trabajo diario en el diseño de máquinas.